Mathematisch elegant ist sie – und in den Augen der Finanzprofis so etwas wie eine Allzweckwaffe. Die Rede ist von der Modernen Portfoliotheorie (MPT). Sie hat die Risiken einer Geldanlage und erzielte Renditen erstmals berechenbar gemacht und stellt damit zweifellos einen Meilenstein in der Börsenforschung dar. Kein Wunder, dass der US-Ökonom Harry Markowitz, der die MPT vor rund 60 Jahren entwickelte, 1990 den Nobel-Gedächtnispreis dafür erhielt.
Doch seither ist viel passiert. Finanzmarktforscher haben in den vergangenen Jahren aufgedeckt, dass die Theorie schwere Mängel aufweist: vor allem unterschätzt die MPT Verlustrisiken dramatisch. Für die Wissenschaft ist das kein Beinbruch,denn es ist üblich, dass ihre Theorien im Laufe der Zeit überarbeitet werden. In diesem Fall hat die Sache jedoch einen Haken: Die Mehrheit der Fondsmanager und Vermögensverwalter vertraut den Gesetzen der MPT noch immer. Millionen Investmententscheidungen werden täglich nach Markowitz’ Regeln gefällt. Das Nachsehen haben Anleger, die diesen Finanzprofis ihr Geld anvertrauen, denn sie gehen sie ein viel zu hohes Risiko ein – unbewusst.
Die Schwächen der MPT sind gar nicht so schwer zu erfassen. Im Kern beschreibt die Theorie, wie Anleger verschiedene Wertpapiere zu optimaler Portfolio-Performance zusammenbauen. Man kann es auch so formulieren: Mit Hilfe der MPT kann ein Portfolio so konstruiert werden, dass es ein optimales Rendite-Risiko-Profil aufweist.
Dabei gilt: Das Verlustrisiko eines Portfolios lässt sich senken, indem man das Geld auf verschiedene Wertpapiere verteilt. Fachleute nennen das Risikostreuung oder Diversifikation. Und: Je mehr Wertpapiere ein Portfolio enthält, desto stärker sinkt das Risiko.
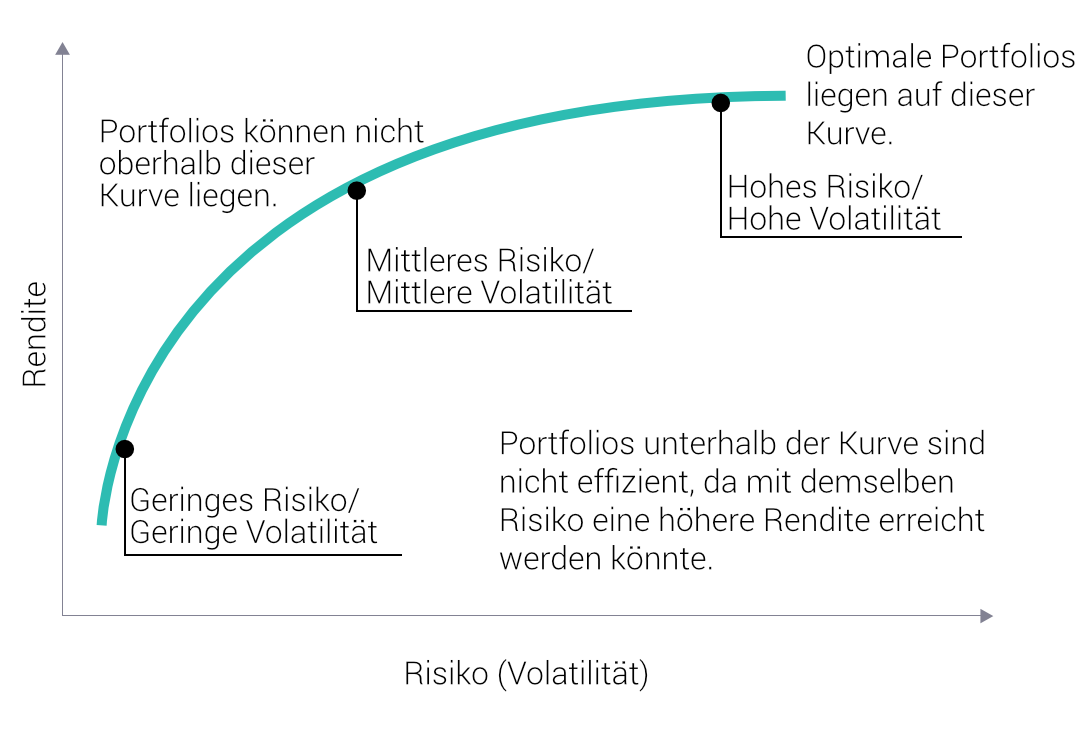
Was aber ein optimales Markowitz-Portfolio ist, lässt sich an Hand einer Grafik zeigen. Sie stellt die Rendite eines Portfolios in Abhängigkeit von dessen Risiko dar. Wichtig dabei: Alle mittels MPT realisierbaren Portfolios liegen auf sowie rechts unterhalb der grünen Kurve. Links oberhalb der Kurve befinden sich Rendite-Risiko-Konstellationen, die unerreichbar bleiben. Damit ist klar: Die Portfolios mit den optimalen Rendite-Risiko-Profilen liegen genau auf der grünen Kurve. Diese Portfolios werden als „effizient“ bezeichnet, denn für jeden Punkt auf der auch „effizienter Rand“ genannten Kurve gilt: Es lässt sich kein Portfolio finden, das bei gleicher Rendite weniger Risiko birgt. Und keines, das bei gleichem Risiko mehr Rendite abwirft.
Im Portfoliomanagement spielt der effiziente Rand eine große Rolle. Denn wenn ein Anleger weiß, welches Risiko er maximal eingehen will, lässt sich daraus das Portfolio mit der maximalen erwarteten Rendite bestimmen. Umgekehrt lässt sich auch das Portfolio mit dem geringsten Risiko bestimmen, wenn der Anleger eine bestimmte Zielrendite vorgibt.
Aber was braucht ein Investor, um optimale Portfolios zu berechnen? Zuerst muss er natürlich das Anlageuniversum kennen, also alle Wertpapiere, die er kaufen kann oder will. Dann sind noch drei Zutaten sind nötig:
Professor Dr. Stefan Mittnik, Lehrstuhlinhaber für Finanzökonometrie an der Ludwig-Maximilians-Universität München, erklärt in dieser Videoreihe wichtige Prinzipien der Modernen Portfoliotheorie.
Zu den Videos
Der Ansatz von Markowitz feierte einen fulminanten Siegeszug in der Investmentbranche. Er lieferte den Finanzprofis, wonach sie sich lange gesehnt hatten: ein einfaches Werkzeug, um Renditen und Risiken von Portfolios zu bestimmen und zu steuern. Doch die MPT konnte die großen Träume der Risikokontrolle nicht erfüllen. Die langjährige Erfahrung zeigt nämlich, dass die Markowitz-Portfolios oft höhere Verluste einfahren als erwartet, weil die Theorie…
Zur Ehrenrettung von Markowitz sei gesagt: Es ist nicht so, dass er nicht rechnen konnte. Warum seine Theorie dann solche Schwächen zeigt? Ganz einfach: Um überhaupt rechnen zu können, musste Markowitz in seinem Modell sehr vereinfachende Annahmen treffen. Das ist in der Wissenschaft üblich. Nur zeigte sich, dass im Fall der MPT Annahmen und Realität sehr weit auseinanderklaffen.
Die wichtigsten Fehlannahmen der MPT sind:
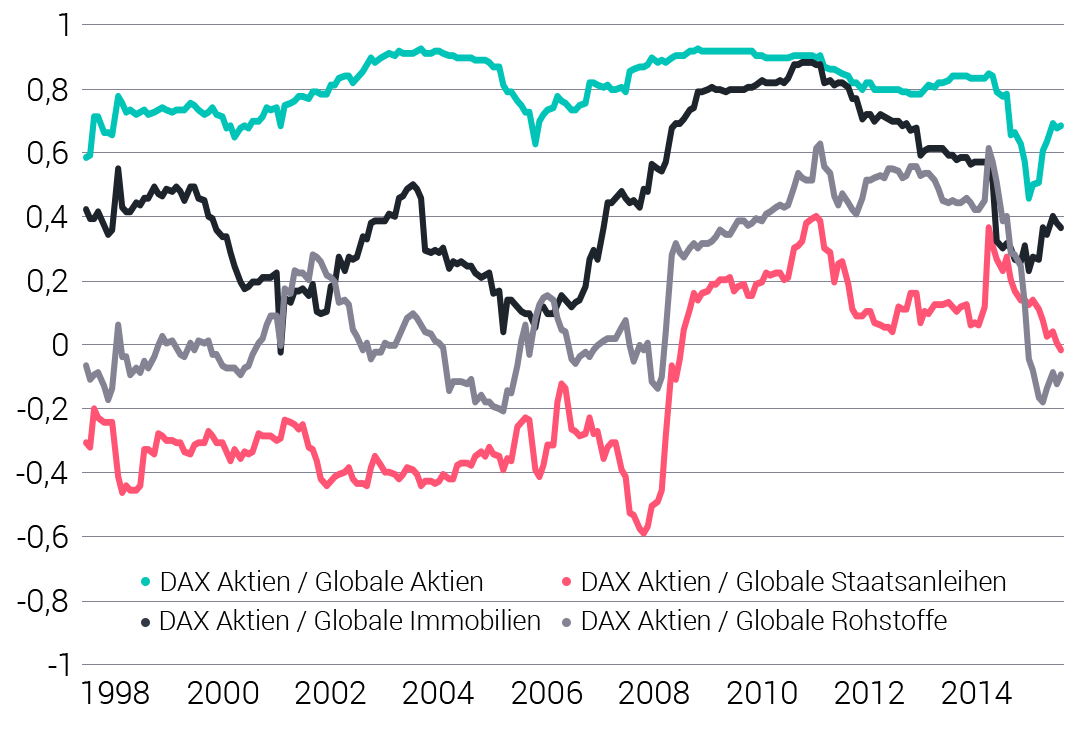
Quelle: Bloomberg
Die Börsenforschung zeigt allerdings: Die Wirklichkeit sieht ganz anders aus. An den Finanzmärkten versagt die Normalverteilungsannahme dramatisch. Die Renditen von Wertpapieren weisen sogenannte „Fat Tails“ auf. Das heißt: Extreme Kurseinbrüche treten viel häufiger auf, als es die Normalverteilung vorgaukelt. Auch sind Gewinne und Verluste nicht symmetrisch verteilt. Obendrein funktioniert die Volatilität als Risikomaß nur in speziellen Fällen wie zum Beispiel der
Normalverteilung. Deshalb werden die Verlustrisiken systematisch unterschätzt (und die Gewinnchancen überschätzt).
Zudem verhalten sich Volatilität und Korrelationen anders als angenommen. Sie hängen von der aktuellen Börsenlage und damit von der Zeit ab. Wann immer die Kurse an der Börse einbrechen, steigen etwa die Korrelationen stark an. Man könnte auch sagen: Wenn Panik an der Börse herrscht, brechen fast alle Kurse gleichzeitig ein. Das hat gravierende Folgen. Denn die Diversifikation beruht darauf, dass man Investments mit möglichst schwachen oder negativen Korrelationen im Portfolio mischt. So soll der Wert von Investment A steigen, wenn der von Investment B fällt und dessen Verluste teilweise ausgleichen – was aber nicht mehr funktioniert, wenn die beiden Investments sich plötzlich im Gleichschritt bewegen, statt wie angenommen konstant negativ korreliert zu sein.
Die Grafik verdeutlicht, wie heftig die Korrelationen in Wirklichkeit schwanken. Sie zeigt die Korrelationen zwischen dem DAX und anderen Anlageklassen über einen Zeitraum von 20 Jahren.
Man sieht: Besonders stark steigen die Korrelationen während der Finanzkrise im Jahr 2008 an. So lag die Korrelation zwischen dem DAX und globalen Staatsanleihen (rote Linie) zu Beginn der Krise noch bei -0,6. Der Wert deutet an, dass sich globale Staatsanleihen besonders gut zur Diversifikation mit DAX-Aktien eignen, weil die Kurse dieser Anleihen steigen sollten, wenn der deutsche Leitindex abstürzt. Im Verlauf der Krise stieg die Korrelation jedoch auf +0,4 an, so dass sich die erhofften Diversifikationseffekte „in Luft auflösten“. Die Diversifikation nach Markowitz versagt genau dann, wenn sie gebraucht wird – wenn es an der Börse kracht.
Die Moderne Portfoliotheorie ist ein allgegenwärtiges Dogma in der Finanzwelt
Bleibt die Frage, warum sich so viele Investmentprofis auf die MPT verlassen, wenn sie so mangelhaft ist. Zum einen, weil die Theorie ein komplexes Problem verführerisch einfach zu lösen scheint. Mit Software, die nach den Gesetzen von Markowitz arbeitet, können Fondsmanager und Vermögensverwalter die Risiken in den Portfolios so komfortabel steuern wie ein Pilot sein Flugzeug. Da drücken sie gern auch mal ein Auge zu, wenn das System Ausfälle zeigt. Zumal ein Crash nicht gleich mit dem Leben bezahlt wird, sondern „nur“ mit finanziellen Verlusten der Kunden. Hinzu kommt, dass sich viele Vermögensverwalter sagen: „Wenn ich wie die gesamte Branche auf die MPT setze, kann ich kaum schlechter abschneiden als die Konkurrenz.“ So lebt die Finanzbranche in einer scheinbar schönen, aber alten Welt mit überholten Regeln.
Für Privatanleger ist das fatal. Sie müssen den laxen Umgang mit den Schwächen der MPT ausbaden. Denn ihnen wird in der Vermögensverwaltung stets zu viel Risiko aufgebürdet – nur weil es sich der Verwalter leicht macht und die Finanzbranche nicht innovativ genug ist, die Mängel der Theorie auszumerzen. Wäre die Autoindustrie ähnlich rückständig, würden die Menschen heute immer noch ohne Airbag, ABS und ESP über die Autobahn rasen – kaum vorstellbar.
Wer die Risiken an den Börsen in den Griff bekommen will, braucht ein besseres Modell als die Markowitz-Theorie. Die gute Nachricht lautet: Solche Modelle gibt es. Die neuen Erkenntnisse der Börsenforschung lassen sich in der Vermögensverwaltung berücksichtigen. Dabei gilt es als erstes, vereinfachende Annahmen wie die Normalverteilung über Bord zu werfen.
Möglich wird das dank modernster Computertechnologie und Simulationsverfahren, die auf realistischeren Annahmen fußen. Dadurch kann das Risiko des Anlegers zuverlässig und vorausschauend, zum Beispiel anhand des Risikomaßes Value-at-Risk (VaR), bestimmt werden. Wichtiger noch: Das Risiko des Klientenportfolios kann möglichst so gesteuert werden, dass es, unabhängig davon, ob es an der Börse gerade ruhig oder turbulent zugeht, im Rahmen der Risikoverträglichkeit des Anlegers bleibt. Denn Ziel sollte es sein, Vermögensverwaltung für den Anleger besser und sicherer zu machen – nicht nur einfach für den Vermögensverwalter.
Der Investmentansatz von Scalable Capital beherzigt die neuen Erkenntnisse der Finanzmarktforschung. Unser Ziel als technologiebasierter Online-Vermögensverwalter – oftmals auch „Robo-Advisor“ gennant – ist es in die besten ETFs (Was sind ETFs?) zu investieren und Klienten bessere risikoadjustierte Renditen zu ermöglichen.
Bild: Unsplash.com
Risikohinweis – Die Kapitalanlage ist mit Risiken verbunden und kann zum Verlust des eingesetzten Vermögens führen. Weder vergangene Wertentwicklungen noch Prognosen haben eine verlässliche Aussagekraft über zukünftige Wertentwicklungen. Wir erbringen keine Anlage-, Rechts- und/oder Steuerberatung. Sollte diese Website Informationen über den Kapitalmarkt, Finanzinstrumente und/oder sonstige für die Kapitalanlage relevante Themen enthalten, so dienen diese Informationen ausschließlich der allgemeinen Erläuterung der von Unternehmen unserer Unternehmensgruppe erbrachten Wertpapierdienstleistungen. Bitte lesen Sie auch unsere Risikohinweise und Nutzungsbedingungen.
Scalable Capital bietet erstklassige Vermögensverwaltung mit einer wegweisenden Investment-Technologie. Global diversifizierte ETF-Portfolios mit modernem Risikomanagement, zu niedrigen Kosten.
